SQL Queries For Mere Mortals: Thinking In Sets Part 2

Sets Continued

• In Part One we talk about concept of sets, operations on sets, started with the first one which is intersection.
• Now in This part we'll complete our journey in sets by talking about the other two operations which are difference and union, so let's start.

Difference

What’s the difference between 21 and 10? If you answered 11, you’re on the right track! A difference operation (sometimes also called subtract, minus, or except) takes one set of values and removes the set of values from a second set. What remains is the set of values in the first set that are not in the second set.

Difference in Set Theory

Let’s take a look at difference in action by examining two sets of numbers.

• The first set of numbers is as follows: 1, 5, 8, 9, 32, 55, 78
• The second set of numbers is as follows: 3, 7, 8, 22, 55, 71, 99
• The difference of the first set of numbers minus the second set of numbers is the numbers that exist in the first set but not the second: 1, 5, 9, 32, 78
• Note that you can turn the previous difference operation around. Thus, the difference of the second set minus the first set : 3, 7, 22, 71, 99

Difference between Result Sets

• To find the difference between two sets of complex set members, you have to find the members that match on all the attributes in the second set with members in the first set.
• Don’t forget that all of the members in each set you’re trying to compare must have the same number and type of attributes.
• Remove from the first set all the matching members you find in the second set, and the result is the difference.
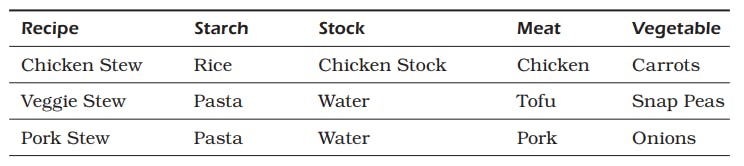
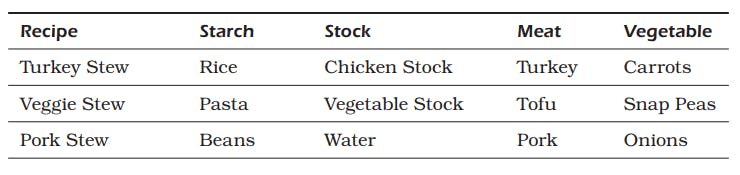
• For example, By recalling the example I mentioned early in Intersection which is the "lunch recipe"
• The difference between My recipes and Mike’s recipes (My minus Mike’s) is all the recipes in My result set that do not appear in Mike’s.

• You can also turn this problem around. Suppose you want to find the recipes in Mike’s result set that are not in my. Here’s the answer:

Difference in Venn Diagram

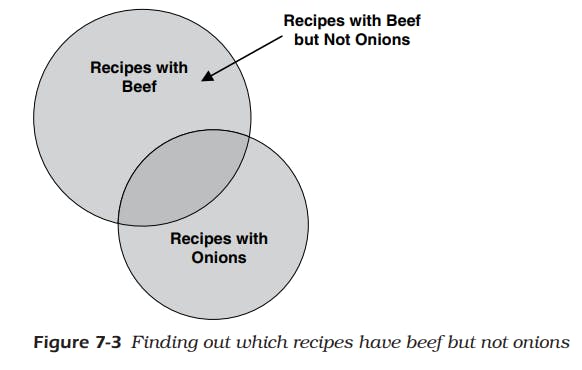
• Let’s assume you have a nice database containing all your favorite recipes. You really do not like the way onions taste with beef, so you’re interested in finding all recipes that contain beef but not onions.
• Figure 7-3 below shows you the set diagram that helps you visualize how to solve this problem.

• The upper full circle represents the set of recipes that contain beef.
• The lower full circle represents the set of recipes that contain onions.
• As you remember from the discussion about INTERSECT, where the two circles overlap is where you’ll find the recipes that contain both.
• The dark-shaded part of the upper circle that’s not part of the overlapping area represents the set of recipes that contain beef but do not contain onions.
• Likewise, the part of the lower circle that’s not part of the overlapping area represents the set of recipes that contain onions but do not contain beef.

Difference In SQL — EXCEPT

Okay, let’s go back to the bicycles and helmets problem again. Let’s say you’re trying to solve this seemingly simple request as follows:
Example:

• Problem statement: “Show me the orders that contain a bike but not a helmet.”
• Translation: Select the distinct order numbers from the order details table where the product number is in the list of bike product numbers and product number is not in the list of helmet product numbers.
• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 11)
  AND ProductNumber NOT IN (10, 25, 26);
  

• Unfortunately, the answer shows you orders that contain only a bike! The problem is that the first IN clause finds detail rows containing a bicycle, but the second IN clause simply eliminates helmet rows.
• If you visualize orders with bicycles and orders with helmets as two distinct sets, you’ll find this easier to understand.
• Figure 7-9 below shows one possible relationship between the two sets of orders.

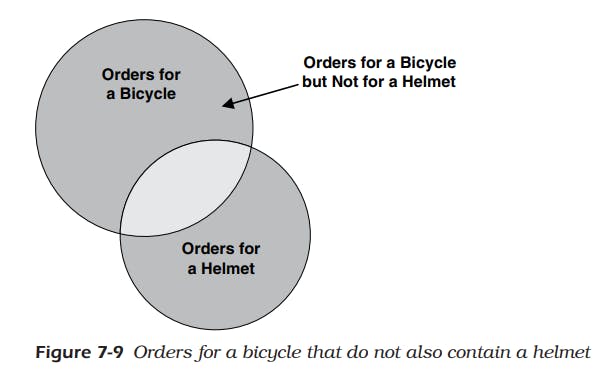
• Seeing “except” or “but not” in your request suggests you’re probably going to have to break the solution into separate sets of data and then link the two sets in some way. (Your request also needs to be broken into two parts.)

The Problem After breaking it into two parts:
Problem 1:

• Problem statement: “Show me the orders that contain a bike.”
• Translation: Select the distinct order numbers from the order details table where the product number is in the list of bike product numbers
• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 11);
  

Problem 2:

• Problem statement: “Show me the orders that contain a helmet.”
• Translation: Select the distinct order numbers from the order details table where the product number is in the list of helmet product numbers
• SQL:

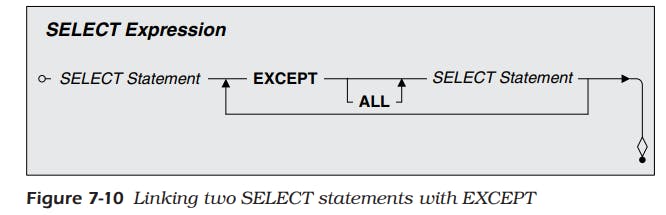
  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (10, 25, 26);
  

• Now you’re ready to get the final solution by using—you guessed it—a difference of the two sets. SQL uses the EXCEPT keyword to denote a difference operation. Figure 7-10 shows you the SQL syntax diagram that handles this problem.

• You can now take the two parts of your request and link them with an EXCEPT operator to get the correct answer:
• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 11)
  EXCEPT
  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (10, 25, 26);
  

• If you want to find out the opposite case orders for helmets that do not include bikes, you can turn it around as follows:
• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (10, 25, 26)
  EXCEPT
  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 11);
  

• The sad news is that not many commercial implementations of SQL yet support the EXCEPT operator. But don't worry I’ll show you an alternative method (OUTER JOIN) in the coming article that can solve this type of problem in another way.

Problems You Can Solve with an Difference

“Show me customers whose names are not the same as any employee.”
“Find all the customers who ordered a bicycle but did not order a helmet.”
“Find the bowlers who had a raw score of 155 or better at Thunderbird Lanes but not at Bolero Lanes.”
“Show me the recipes that have beef but not garlic.”

Union

• Union lets you combine two sets of similar information into one set.
• The union of two sets A and B is defined as the set of all the elements which lie in set A and set B or both the elements in A and B altogether.

Union in Set Theory

• Let’s take a look at union in action by examining two sets of numbers.
• The first set of numbers is as follows: 1, 5, 8, 9, 32, 55, 78
• The second set of numbers is as follows: 3, 7, 8, 22, 55, 71, 99
• The union of these two sets of numbers is the numbers in both sets combined into one new set: 1, 5, 8, 9, 32, 55, 78, 3, 7, 22, 71, 99
• that the values common to both sets, 8 and 55, appear only once in the answer.
• Also, the sequence of the numbers in the result set is not necessarily in any specific order.
• When you ask a database system to perform a UNION, the values returned won’t necessarily be in sequence unless you explicitly include an ORDER BY clause.
• In SQL, you can also ask for a UNION ALL if you want to see the duplicate members.

Union between Result Sets

• The members of each set don’t have to be just single values.
• To find the union of two or more sets of complex members, all the members in each set you’re trying to union must have the same number and type of attributes.
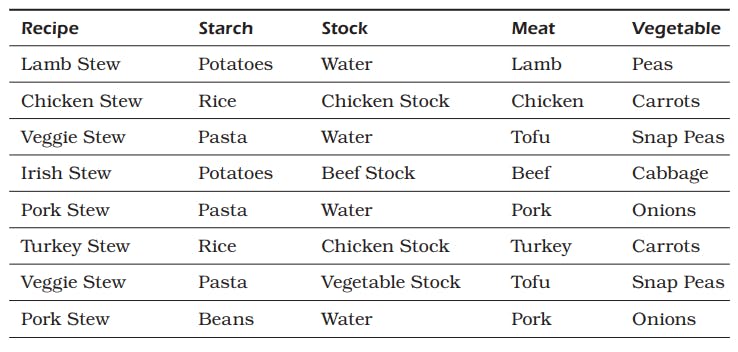
• Recalling the "lunch recipe" example
• The union of these two sets is all the rows in both sets as shown in the figure below:

Union in Venn Diagram

• Let’s assume you have a nice database containing all your favorite recipes. You really like recipes with either beef or onions, so you want a list of recipes that contain either ingredient.
• Figure 7-5 below shows you the set diagram that helps you visualize how to solve this problem.

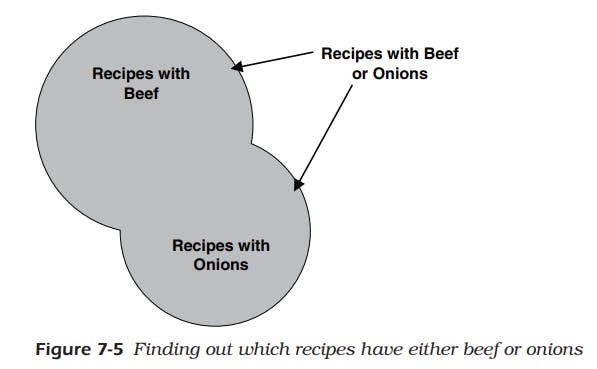
• The upper circle represents the set of recipes that contain beef.
• The lower circle represents the set of recipes that contain onions.
• The union of the two circles gives you all the recipes that contain either ingredient, with duplicates eliminated where the two sets overlap.

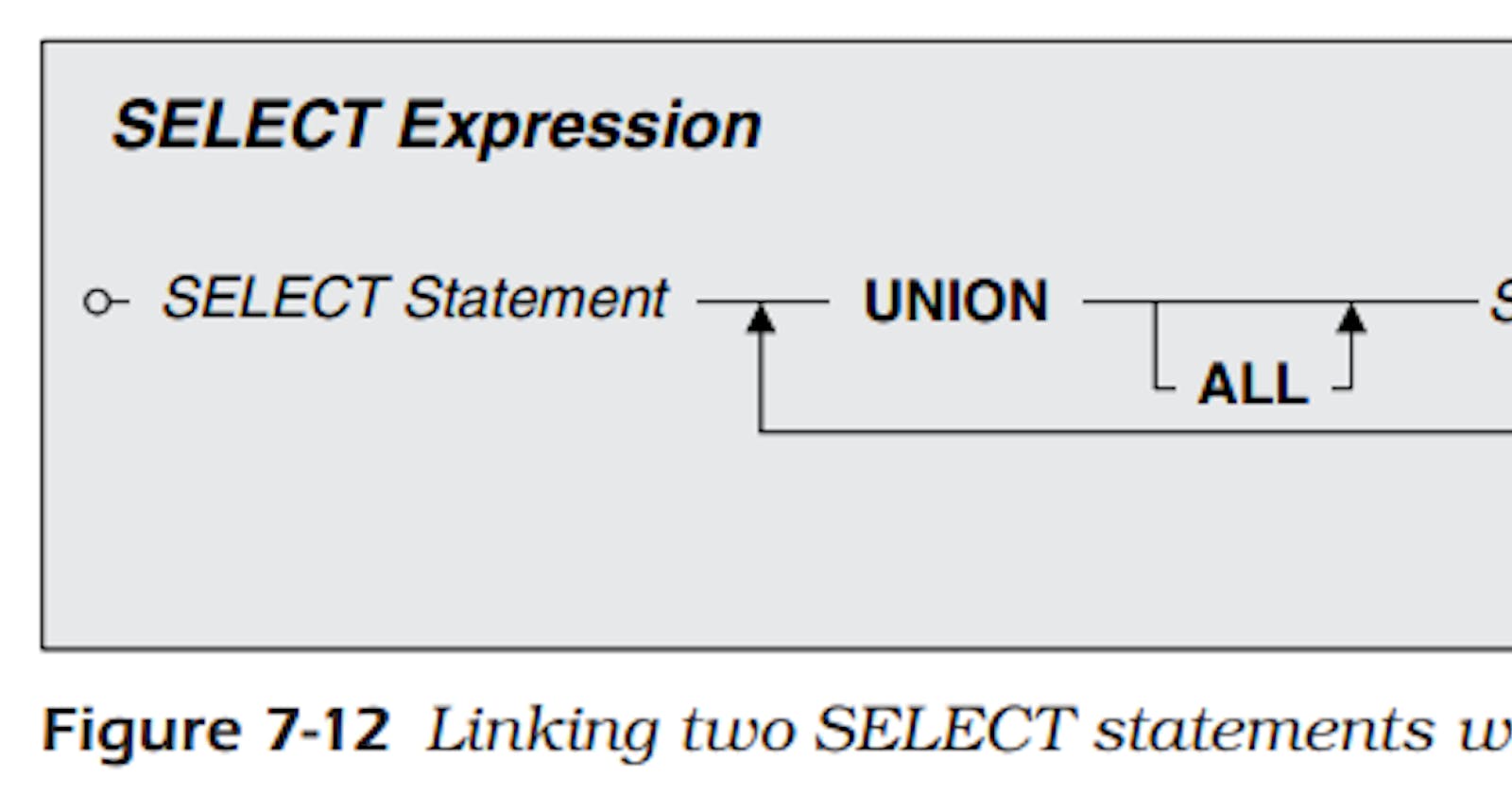
Union In SQL — UNION (Combining Sets)

• One more problem about bicycles and helmets, then i promise you I’ll pedal on to the next chapter.
• Let’s say you’re trying to solve this request, which looks simple enough on the first look:

Example:

• Problem statement: “Show me the orders that contain either a bike or a helmet.”
• Translation: Select the distinct order numbers from the order details table where the product number is in the list of bike and helmet product numbers.
• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 10, 11, 25, 26);
  

• Actually, that works just fine! So why use a UNION to solve this problem? The truth is, you probably would not. However, if I make the problem more complicated, a UNION would be useful:

  “List the customers who ordered a bicycle together with the vendors who provide bicycles.”

• Unfortunately, answering this request involves creating a couple of queries using JOIN operations, then using UNION to get the final result.

• Because I haven’t shown you how to do a JOIN yet, I’ll save solving this problem for a coming article . Gives you something to look forward to, doesn’t it?

• Solving the bike and helmet problem using UNION:

• SQL:

  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (1, 2, 6, 11)
  UNION
  SELECT DISTINCT OrderNumber
  FROM Order_Details
  WHERE ProductNumber IN (10, 25, 26);
  

• The good news is that nearly all commercial implementations of SQL support the UNION operator.
• As is perhaps obvious from the examples, a UNION might be doing it the hard way when you want to get an “either-or” result from a single table.
• UNION is most useful for compiling a list from several similarly structured but different tables. I’ll explore UNION in much more detail in a coming article.

Problems You Can Solve with an Union

• A union lets you “mush together” rows from two similar sets, with the added advantage of no duplicate rows.

• Here’s a sample of the problems you can solve using a union technique with data from the sample databases:

  “Show me all the customer and employee names and addresses.”
  “List all the customers who ordered a bicycle combined with all the customers who ordered a helmet.”
  “Show me the recipes that have beef together with the recipes that have garlic.”
  “Show me the students who have an average score of 85 or better in Art together with the students who have an average score of 85 or better in Computer Science.”

• As with other “pure” set operations, one of the limitations is that the values must match in all the columns in each result set.

• This works well if you’re unioning two or more sets from the same table—for example, customers who ordered bicycles and customers who ordered helmets.
• It also works well when you’re performing a union on sets from tables that have like columns—for example, customer names and addresses and employee names and addresses.